


Steps:
A.) To get the area of the picture, you have to multiply 18 cm x 18 cm and you'll get 324 cm2.
B.) To get the area of the board, you have to multiply the area of the book, which is 324 cm2 to 4 so, 324 cm2 multiply 4 because it says that the area of the picture is 4 times of the area of the board so the answer is 1296 cm2.
C.) To get the dimension of the board or the side length of the board you have to find the square root of 1296 cm2 which is 36 cm. To find the the square root of 1296 use the square root sign in your calculator and type in 1296 then you'll exactly get 36 cm.
#18 Question: Extend Question.

Steps:
A.) An easy way of finding the square root of 9 is to do the prime factorization method and when a number is multiplied by itself it means its squared.
B.) To get the square root of 3, you have to find the 2 closest perfect square to 3 which is 1 and 4. Then find the half way between. Then, think which of the 2 closest perfect square is really close to 3 which is 4 but, 3 comes before 4 so the answer should be 1 and something.
C.) to get the square root of 3, use the square root sign in your calculator and type 3. Then after press the equal sign. I am sure that you'll get 1.732050808 but, you have to round it to the nearest tenths so it would be 1.7 .
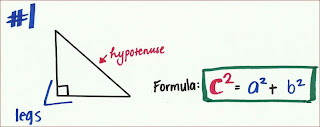
The variable "a" and "b" represents the 2 legs of a right triangle. "C", furthermore represents the "longest side" of a right triangle or also known as the "hypotenuse".A "pythagorean relationship" is a relationship in which we're finding the length of each side of a right triangle and in which we're finding the area of the right triangle. In addition, "pythagorean relationship" helps you to show or to prove if a triangle is a "right" triangle. You'll know if a triangle is a "right" triangle when the variable "a" and "b" adds up the answer for the variable "c" or the "hypotenuse".


Good Job Tinille.
ReplyDeleteOne thing i really like about your post is that you show each steps which is helpful.
Super great job Tinille! Your blog post was perfect! I liked how you used your photography skills and even added the calculator to make it look more eye catching! Also in the beginning, you showed us facts about square rooting and square numbers which I found very amusing and made it look 10x more professional looking. Also, your use in colours for the fonts were outstanding! I liked how you used your time to just make the word steps, A), B), and C) a different colour. Speaking of steps, I liked how you split your answer in steps so it would be easier for us to understand. It was very efficient. Your use of colours in the pictures also showed creativity and I liked how you put the question in your picture and put an image to help indicate what you were talking about. Because of that, it took less pictures and it made it more clearer and made it seem less boring to read. Your game was very entertaining and if only that game were real in real life right? I also found your video helpful. Overall you did a marvellous job on your blog post. Keep up the extravagant work Tinille! =)
ReplyDelete